문제
RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.
집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.
- 1번 집의 색은 2번 집의 색과 같지 않아야 한다.
- N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
- i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.
입력
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.
문제 링크 : RGB거리
설명
해당 문제는 DP를 이용해서 풀 수 있다.
시간제한이 0.5초이고 최대 N이 1,000이므로 O(n)으로 풀어야겠다고 생각했다.
문제 설명을 보면 규칙이 있는데 사실 1번, 2번, 3번 다 동일한 설명이라고 생각한다.
N = 3일 경우에 i가 2라고 하자.
그럼 그림과 같은 상태일 것이다.
일단 1번과 2번의 조건에 부합하려면 2번째 집은 빨강이 될 수 없다. 그럼 선택지는 초록과 파랑이 남는다.
여기서 초록을 고른다고 하자.

그럼 이런 상태가 될 것이고 i는 현재 3일 것이다.
i -1번째(2번째) 집과 색이 달라야하므로 초록을 빼고 빨강과 파랑 중에서 고를 수 있다.
둘 중 어느것을 골라도 1번, 2번, 3번 조건에 부합한다.
빨강을 고르더라도 i가 2일 때 기준으로 보면 i -1(1번째) = 빨강 i + 1(3번째) = 빨강 i(2번째) = 초록이므로 색이 다르기에.
그러므로 조건1,2,3은 다 같은 말이 된다.
혹시 알아챘을 수도 있겠지만 이 문제의 최솟값을 구하는 방법은 조건을 살짝 참고하면 구할 수 있다.
예제 1번으로 구해보자.
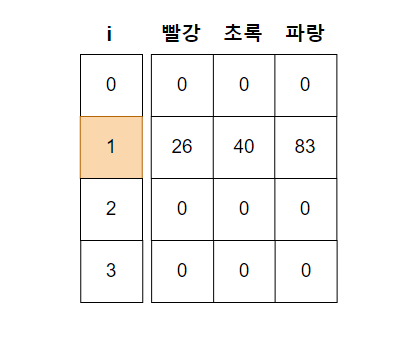
현재 i = 1인 경우에 어떠한 색을 골라도 예제 그대로 값이 나올 것이다. 처음이기 때문에.
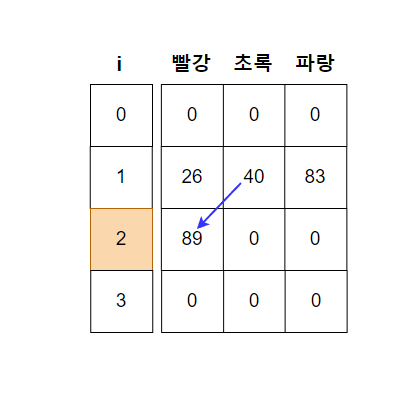
i = 2인 경우부터 중요한데 만약 빨강을 고르게 될 경우 i -1(1번째 집)에서 빨강을 고르지 않았을 경우에만 가능하므로 i -1(1번째 집)에서 고른 초록(40), 파랑(83) 값 중 최솟값을 가져와 현재 i(2번째 집)의 빨강 값과 더해준다. 49 + 40 = 89
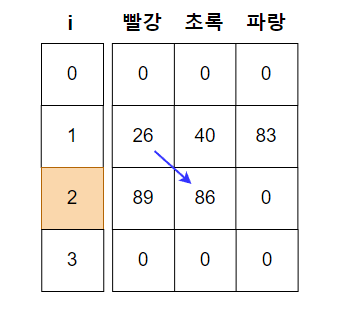
초록을 고르게 될 경우 i -1(1번째 집)에서 초록을 고르지 않았을 경우에만 가능하다.
그러므로 i -1(1번째 집)의 빨강(26), 파랑(83) 값 중 최솟값을 가져와 i(2번째 집) 초록 값과 더해준다. 26 + 60 = 86
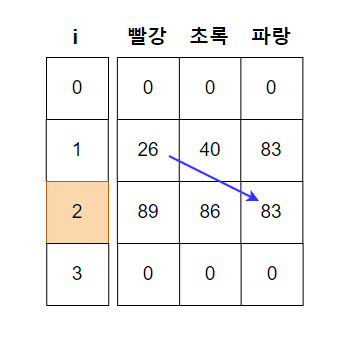
파랑의 경우 i -1(1번째 집)에서 파랑을 고르지 않았을 경우에만 가능하므로 i -1(1번째 집) 빨강, 초록 값 중 최솟값을 가져와 i(2번째 집)의 파랑 값과 더해준다. 26 + 57 = 83
위와 같이 나머지도 채우면 아래와 같은 값이 최종적으로 나오게 된다.
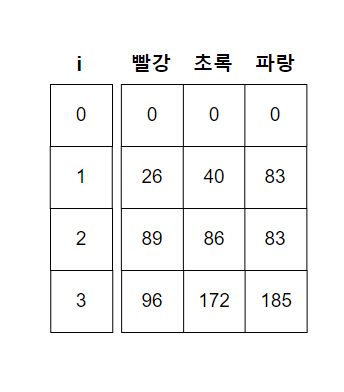
여기서 최솟값을 출력하면 정답이 된다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[1001][3];
int[][] dp = new int[1001][3];
int ans = 0;
for (int i = 1; i<=n; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
arr[i][2] = Integer.parseInt(st.nextToken());
}
for (int i = 1; i <=n;i++){
dp[i][0] = Math.min(dp[i -1][1], dp[i-1][2]) + arr[i][0]; // 빨강
dp[i][1] = Math.min(dp[i -1][0], dp[i-1][2]) + arr[i][1]; // 초록
dp[i][2] = Math.min(dp[i -1][0], dp[i-1][1]) + arr[i][2]; // 파랑
ans = Math.min(dp[i][0], Math.min(dp[i][1], dp[i][2])); // 최솟값 저장
}
System.out.println(ans);
}
}
'알고리즘' 카테고리의 다른 글
| [Java] 백준 30974 What's your ETA? (2) | 2023.12.28 |
|---|---|
| [Java] 백준 30970 선택의 기로 (0) | 2023.12.24 |
| [Java] 백준 1003 피보나치 함수 (0) | 2023.12.21 |
| [Java] 백준 27127 수 나누기 게임 (1) | 2023.12.20 |
| [Java] LeetCode 70. Climbing Stairs (0) | 2023.12.18 |

