문제
떤 동물원에 가로로 두칸 세로로 N칸인 아래와 같은 우리가 있다.
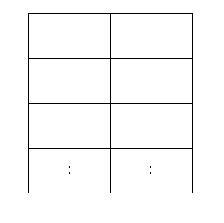
이 동물원에는 사자들이 살고 있는데 사자들을 우리에 가둘 때, 가로로도 세로로도 붙어 있게 배치할 수는 없다. 이 동물원 조련사는 사자들의 배치 문제 때문에 골머리를 앓고 있다.
동물원 조련사의 머리가 아프지 않도록 우리가 2*N 배열에 사자를 배치하는 경우의 수가 몇 가지인지를 알아내는 프로그램을 작성해 주도록 하자. 사자를 한 마리도 배치하지 않는 경우도 하나의 경우의 수로 친다고 가정한다.
입력
첫째 줄에 우리의 크기 N(1≤N≤100,000)이 주어진다.
출력
첫째 줄에 사자를 배치하는 경우의 수를 9901로 나눈 나머지를 출력하여라.
문제 링크 : 동물원
설명
저번 달까지만 해도 점화식도 못 세우고 문제 감도 못 잡아서 못 풀었던 문제였는데 오늘 20분만에 내 힘으로 풀었다...!
ㅠㅠㅠ 한달만에 이렇게 달라졌나 싶고 뿌듯하다
문제는 간단하다 사자를 넣었을 때 가로와 세로가 겹치지 않게 넣을 수 있는 경우의 수를 구하면 된다.
그림으로 보면 이런 의미이다.
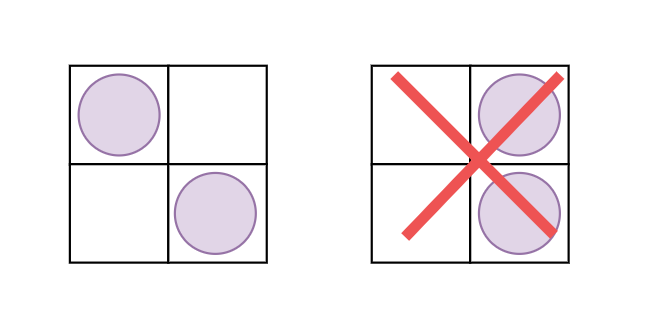
그림처럼 N=2 크기의 우리가 있을 때, 1번째 왼쪽에 사자를 넣은 상황이다.
문제에서 가로와 세로에 붙어서 배치할 수 없다고 했기 때문에 왼쪽 그림처럼 오른쪽에 사자를 넣으면 올바른 경우이다.
반면 오른쪽 그림처럼 붙어서 배치하면 이 경우는 성립할 수 없는 경우가 된다.
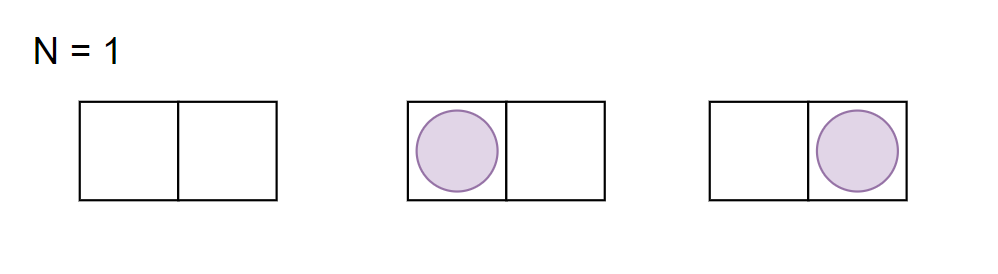
먼저 N이 1일 경우는 사자를 넣지 않는 경우, 왼쪽으로 넣은 경우, 오른쪽으로 넣은 경우
총 3가지의 경우의 수가 나올 수 있다.
N이 2일 경우 아래와 같은 경우의 수가 나올 수 있다.
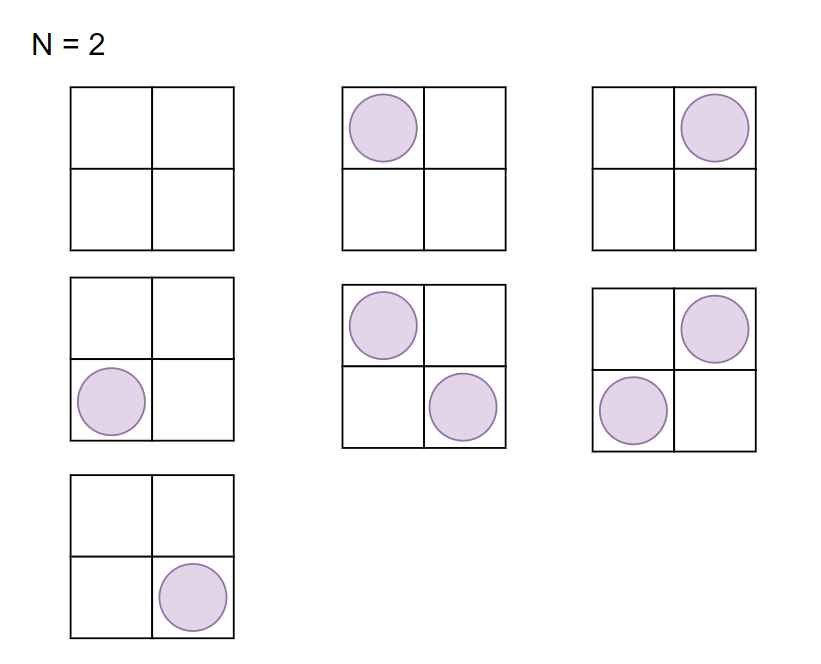
특징이 보일 수도 있고 보이지 않을 수도 있다.
일단 맨 왼쪽의 경우의 수는 n-1인 1번째 칸에 사자를 넣지 않은 경우이다.
1번째 칸에 사자를 넣지 않았으므로 2번째 칸은 본인의 칸에 사자를 넣지 않은 경우, 왼쪽에 넣은 경우, 오른쪽에 넣은 경우 => 총 3가지 경우를 만들 수 있다.
가운데 경우의 수는 n-1인 1번째 칸에서 왼쪽에 사자를 넣은 경우이다.
이때 두번째 칸에서 가능한 선택지는 사자를 넣지 않거나, 1번과 겹치지 않게 오른쪽에 사자를 넣는 경우 => 총 2가지 경우를 만들 수 있다.
맨 오른쪽의 경우는 n-1 인 1번째 칸에 사자를 오른쪽으로 넣은 경우이다.
이 때 두번째 칸에서 가능한 선택지는 사자를 넣지 않거나 왼쪽에 넣는 경우 => 총 2가지 경우를 만들 수 있다.
이런식으로 n만큼 경우의 수를 만들면 그것이 답이 된다.
예제 1인 4까지 그림으로 보여드리기에는 너무 경우의 수가 많이 나와서 만들지 못했다...
나는 2차원 배열로 dp를 세웠는데 풀고 다른 사람의 코드를 보니 충분히 1차원으로도 가능했다.
위 아이디어로 점화식을 짜면 아래와 같이 완성이 된다.
| n \ 사자 | 1 | 2 | 3 |
| 1 | 1 | 1 | 1 |
| 2 | 3 | 2 | 2 |
| 3 | 7 | 5 | 5 |
| 4 | 17 | 12 | 12 |
나는 2차원 배열로 해서 2차원이지만 1차원으로도 충분히 가능!
1차원으로 표현하면 아래와 같이 된다.
| n | 1 | 2 | 3 | 4 |
| 3 | 7 | 17 | 41 |
점화식으로 봤을 때 특징이 더 잘보인다.
잘 보면 n -2 + n - 1 * 2을 더한 값이 현재 dp값이라는 것을 알 수 있다.
위 1차원 배열로 봤을 때 n = 3 의 값을 구한다면 3 + (7 * 2) = 17이 나온다.
이렇게 간단한 점화식이...ㅠ
내가 짠 2차원 배열은 아주 단순하다.
그냥 [0] 번째는 사자를 넣지 않았을 때를 생각하고 n-1번째의 모든 경우의 합을 넣어주고
[1] 번째는 사자를 왼쪽에 넣었을 때를 생각하고 n-1번째의 [0]번째와 [1]번째의 합을 넣어줬다.
그리고 [2]번째에는 사자를 오른쪽에 넣었을 때 n-1번째의 [0] 번째와 [2]번째의 합을 넣어줬다.
왜 n-1의 [0]번째와 [1]번째의 합을 넣는가?
현재 우리의 경우의 수를 찾기 위해서는 앞의 우리의 경우의 수가 필요하다.
현재 우리의 왼쪽에 사자를 넣을 경우 앞의 우리에서 사자를 넣지 않는 경우의 수 + 왼쪽에 사자를 넣은 경우의 수 를 합한게 현재 우리에서의 경우의 수가 된다.
음 글로 말하니 조금 이해가 안될 수도 있을 것 같다.
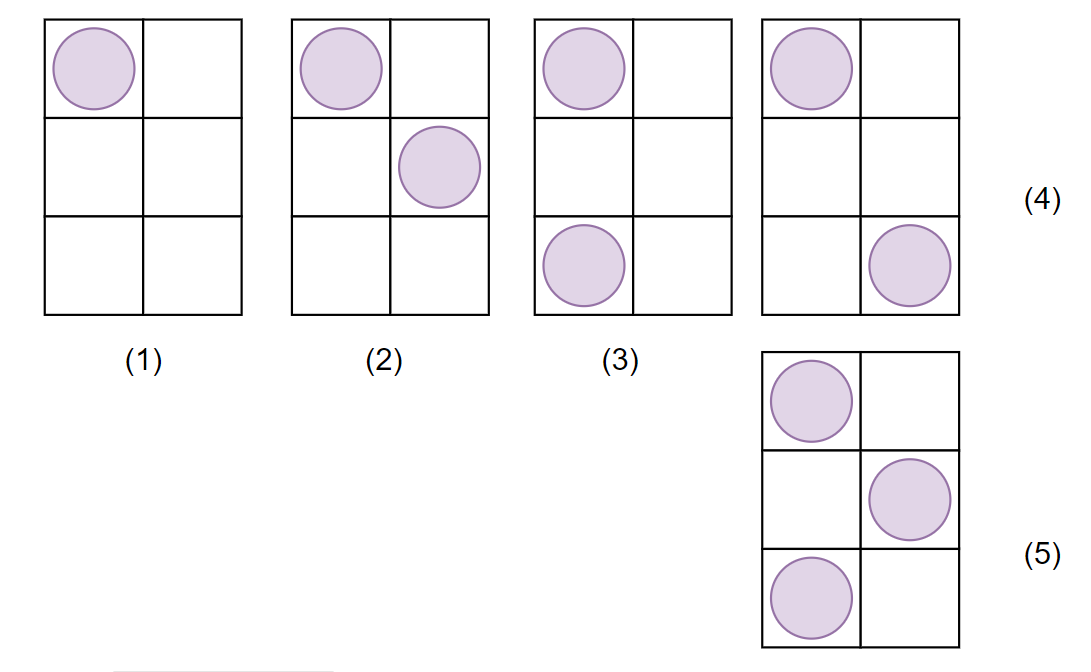
현재 n = 3이고 첫번째 왼쪽우리에 사자가 있는 경우이다.
5번째의 경우를 제외하면 2번째와 3번째에 사자를 넣지 않는 경우, 3번째에 사자를 넣지 않는 경우, 2번째에 사자를 넣지 않는 경우*2 가 된다. 그리고 마지막에 2번째와 겹치지 않도록 왼쪽에 사자를 넣을 수 있는 경우 => 5가지 가 된다.
위 그림에서 보면 3번째의 왼쪽 경우의 수를 구하기 위해 2번째에서 사자를 넣지 않은 경우 + 2번째에서 사자를 왼쪽에 넣은 경우의 합 = 3번째 경우의 수인 것을 알 수 있다.
그러므로 현재 우리의 왼쪽 값을 구할 때 n-1의 사자를 넣지 않은 경우와 왼쪽만 넣은 경우를 합치는 것이다.
코드
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
long [][] dp = new long[n +1][3];
dp[1][0] = dp[1][1] = dp[1][2] = 1;
for (int i = 2; i <= n; i++){
// n -1 모든 경우의 수
dp[i][0] = (dp[i -1][0] + dp[i -1][1] + dp[i -1][2]) % 9901;
// n -1의 사자 0마리 경우의 수 + 사자 왼쪽 경우의 수
dp[i][1] = (dp[i -1][0] + dp[i -1][1]) % 9901;
// n -1의 사자 0마리 경우의 수 + 사자 오른쪽 경우의 수
dp[i][2] = (dp[i -1][0] + dp[i -1][2]) % 9901;
}
System.out.println((dp[n][0] + dp[n][1] + dp[n][2]) % 9901);
}
}
'알고리즘' 카테고리의 다른 글
| [Java] 백준 13021 공 색칠하기 (0) | 2024.03.10 |
|---|---|
| [Java] 백준 8911 거북이 (2) | 2024.02.14 |
| [Java] 백준 3085 사탕 게임 (0) | 2024.02.06 |
| [Java] 백준 17281 ⚾ (1) | 2024.01.27 |
| [Java] 백준 1092 배 (0) | 2024.01.22 |

