문제
n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
입력
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 경우의 수를 출력한다. 경우의 수는 231보다 작다.
문제 링크 : 동전 1
설명
주어진 N개의 동전을 사용해서 K를 만들 수 있는 경우의 수를 구하는 문제이다.
처음에 규칙을 잘못 찾아서 "음?" 했던 문제이다...
주어진 동전으로 K까지 가능한 경우의 수를 봤어야 했는데 나는 K로 가면서 동전이 사용되는 갯수를 보아서 규칙을 찾을 수 없었다.

현재 동전 1인 경우 K(10) 까지 가능한 경우의 수는 1가지이다.
1 = 1 / 2 = 1+1 / 3 = 1+1+1 ....
그럼 다음 동전을 보자

2원의 동전일 경우 1원은 만들 수 없다. 그러므로 전 값을 그대로 가져온다.
2원으로 2원을 만드는 경우는 1가지이다. (2원 하나를 사용할 때) 그리고 앞에 동전의 경우의 수와 (1원의 동전으로 만들 수 있는 경우의 수)와 더해준다.

2원의 동전으로 3원을 만들 수 있는 경우는 1가지이다. (2원 + 1원)
그러므로 앞에 동전의 경우의 수(1원의 동전으로 3을 만드는 경우의 수) 와 2원의 경우의 수를 더해준다.

4원을 만드는 경우 2원의 동전으로 가능한 경우의 수는 2가지가 된다. (2+2, 2+1+1)
앞에 동전으로 만들을 수 있는 경우의 수와 2원의 동전으로 만들 수 있는 경우의 수를 합쳐준다.
이러한 규칙을 반복하여 K(10) 까지 반복하면 아래처럼 완성이 된다.
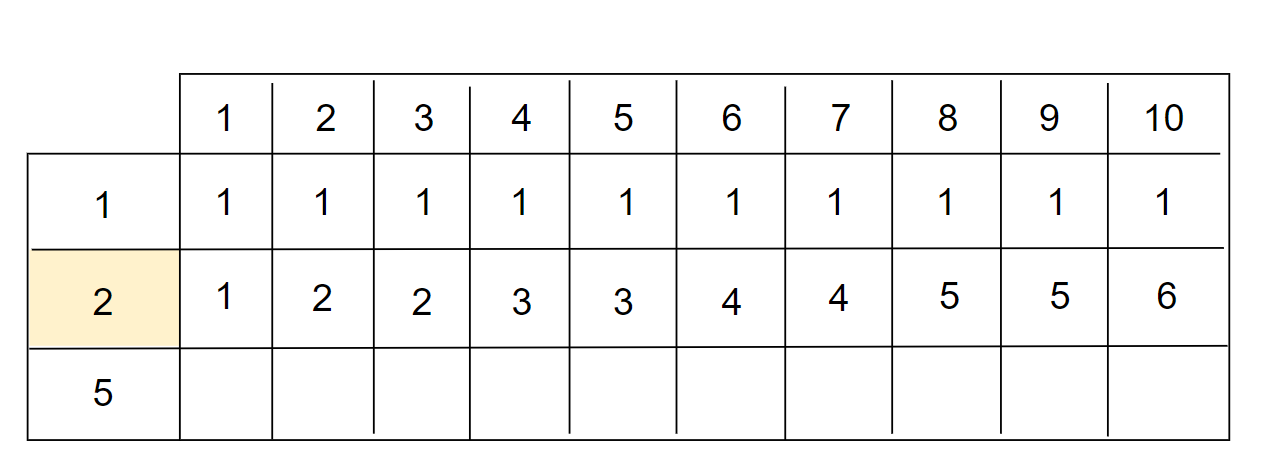
2원의 동전과 같은 방법으로 5원의 동전 경우의 수도 구해준다.

5원의 동전의 경우의 수까지 구해줬을 때 마지막 값이 최종 경우의 수가 된다.
따라서 답은 10이 되겠다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); int k = Integer.parseInt(st.nextToken());
// 최종 값이 커질 것을 대비하여 long으로 선언하였으나 문제에 2^31이상의 값은 나오지 않는다고 설명.
long[] dp = new long[k + 1];
int[] coin = new int[n + 1];
for (int i = 1; i <= n; i++){
coin[i] = Integer.parseInt(br.readLine());
}
dp[0] = 1; // 초기값 설정
for (int i = 1; i <= n; i++) {
for (int j = coin[i]; j <= k; j++){ // 현재 코인의 값이 k보다 작을 경우에만 경우의 수 구해줌
// j에서 숫자를 키워가며 현재 동전 - 커지는 숫자 = 그 값과 더해줌
dp[j] += dp[j - coin[i]];
}
}
System.out.println(dp[k]);
}
}'알고리즘' 카테고리의 다른 글
| [Java] 백준 11051 이항 계수2 (0) | 2024.01.09 |
|---|---|
| [Java] 백준 2294 동전 2 (1) | 2024.01.06 |
| [Java] 백준 9461 파도반 수열 (0) | 2023.12.30 |
| [Java] 백준 1916 최소비용 구하기 (0) | 2023.12.29 |
| [Java] 백준 1912 연속합 (0) | 2023.12.28 |

